Ya en otra entrada os hablé de cómo se podía medir una estructura histológica a través de una foto de microscopía óptica, hoy vamos a hablar de algo parecido pero utilizando otro método para averiguar la medida.
El otro día estaba observado unos cortes del testículo de la rata, y me llamó mucho la atención que el diámetro de los tubos seminíferos era más o menos constantes, casi todos tenían un diámetro parecido. ¿Pero cuál era su diámetro real? Me puse manos a la obra e hice fotos de diferentes zonas del corte a 40 y a 100 aumentos (x4, x10). Y en lugar de utilizar una escala milimétrica para comparar los segmentos como hice la última vez decidí utilizar un programa informático llamado ImageJ 1.41f: Es totalmente gratuito y está disponible para todos los S.O.
Este programa, entre otras muchas aplicaciones, permite definir los parámetros utilizados en el microscopio, es decir, el número de aumentos utilizados, así como seleccionar el zoom utilizado en la cámara de fotos. En mi caso una simple cámara digital me permitió sacar estas fotos ayer:
En total 6 fotos a partir de las cuales he realizado las medidas, en total 100 medidas, para tener un muestreo aceptable. No obstante hay que tener en cuenta que las medidas se han realizado en un corte de testículo de un solo ratón, y que por tanto para que la medida media obtenida pudiese representar el estándar deberíamos analizar diferentes cortes y de diferentes ratones que hayan vivido en las mismas condiciones. No obstante es una aproximación ya que el resultado obtenido no es ni mucho menos contradictorio con lo que hay publicado en las bibliografías que he podido consultar.
Los datos están en micras (10^-6 m), aquí aparecen en una tabla todas las medidas realizadas y a continuación los datos estadísticos de dichas medidas tratadas mediante el software de estadística SPSS 14.0:
281,29 197,54 197,54 275,30 185,04 141,33 141,48 158,16 194,52 159,22 158,30 181,19 181,77 183,39 177,63 187,05 167,30 158,51 139,33 181,10 140,76 175,52 148,09 216,89 150,73 163,03 137,72 158,93 160,93 140,70 162,33 184,68 173,05 211,00 179,72 143,94 181,05 158,93 182,14 182,71 193,28 148,63 278,78 157,70 190,81 190,55 208,72 150,68 151,68 186,97 173,08 174,46 172,50 180,73 180,19 160,93 178,39 160,98 172,77 146,69 178,72 140,83 174,65 144,48 161,00 188,06 154,92 164,45 164,11 140,25 184,57 140,59 166,23 182,04 162,85 143,49 166,14 157,02 263,48 208,74 174,07 226,39 209,44 153,80 201,03 186,54 220,32 211,27 184,09 191,36 161,81 179,50 174,41 152,65 199,07 135,84 202,95 177,58 140,02 228,03
Estadísticos diámetro de los túbulos
| N Válidos | 100 |
| Perdidos | 1 |
| Media | 176,5515 |
| Error típ. de la media | 2,96346 |
| Mediana | 174,4350 |
| Desv. típ. | 29,63461 |
| Varianza | 878,210 |
| Asimetría | 1,440 |
| Error típ. de asimetría | ,241 |
| Curtosis | 3,006 |
| Error típ. de curtosis | ,478 |
| Rango | 145,45 |
| Mínimo | 135,84 |
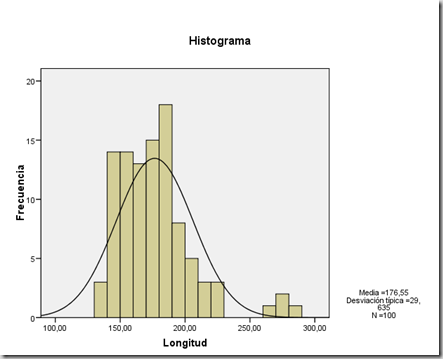
Como vemos la media obtenida es de 176,55 micras, en la bibliografía dice que el diámetro de los túbulos seminíferos de rata es de unas 200 micras, por tanto parece ser que no nos hemos alejado demasiado.
Aquí tenéis otro ejemplo de como tratar los datos que nos proporcionan unas simples fotografías de microscopía óptica, eso sí para que los datos fuesen fiables, estadísticamente deberíamos medir el diámetro de diferentes individuos y comparar medias mediante nuevas fórmulas estadísticas.

No hay comentarios :
Publicar un comentario